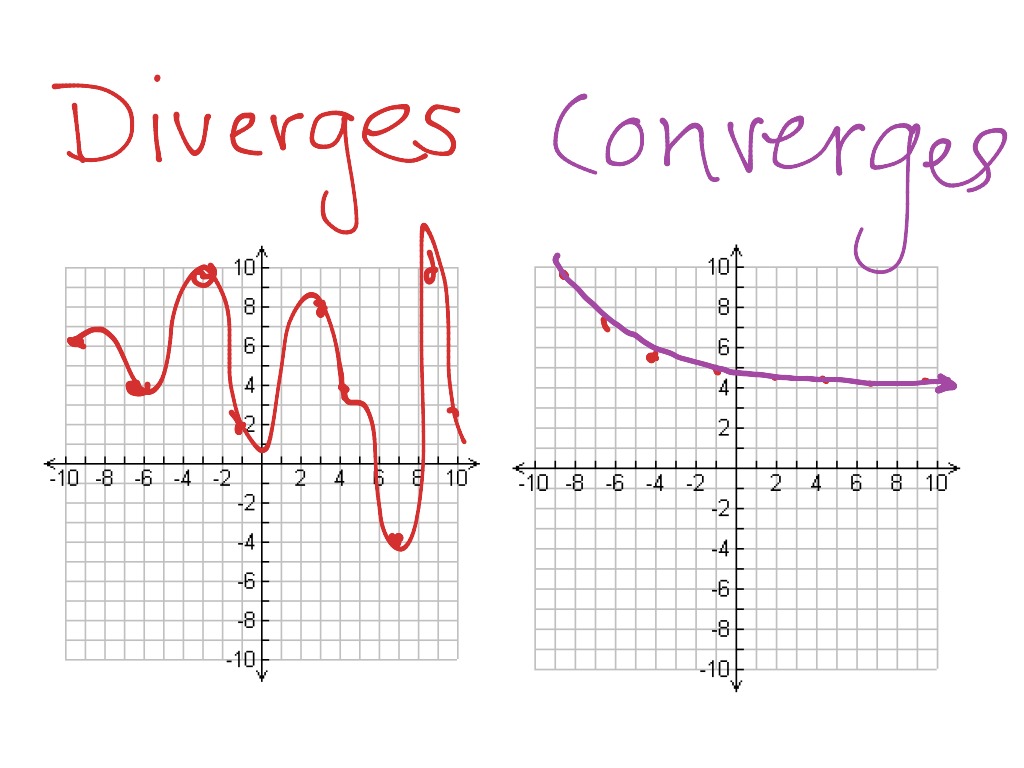
Converge In Math
Converge In Math - In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. Something diverges when it doesn't converge. We will illustrate how partial.
Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. We will illustrate how partial. In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.
We will illustrate how partial. Something diverges when it doesn't converge. In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually.
Integral Test
Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial.
Proving a Sequence Converges Advanced Calculus Example Calculus
Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. Something diverges when it doesn't converge. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.
[Resuelta] analisisreal ¿Por qué la convergencia es
In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. We will illustrate how partial. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. Something diverges when it doesn't converge.
Solved Determine whether the series is convergent or
We will illustrate how partial. Something diverges when it doesn't converge. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.
Higher Maths 1.4 Sequences
In this section we will discuss in greater detail the convergence and divergence of infinite series. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. We will illustrate how partial. Something diverges when it doesn't converge.
Sequences Convergence and Divergence YouTube
In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge. We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually.
Converging and Diverging Sequences Using Limits Practice Problems
We will illustrate how partial. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. Something diverges when it doesn't converge. In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.
Week 1 sequence/general term/converge or diverge Math, Calculus
We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge.
Ex Determine if an Infinite Geometric Series Converges or Diverges
In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. We will illustrate how partial. In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually.
All types of sequences in math bkjery
Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Something diverges when it doesn't converge. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial.
Notoriously The Series $$\Sum_{K=1}^{\Infty} (\Frac{1}{N})$$ Actually.
In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge. We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.
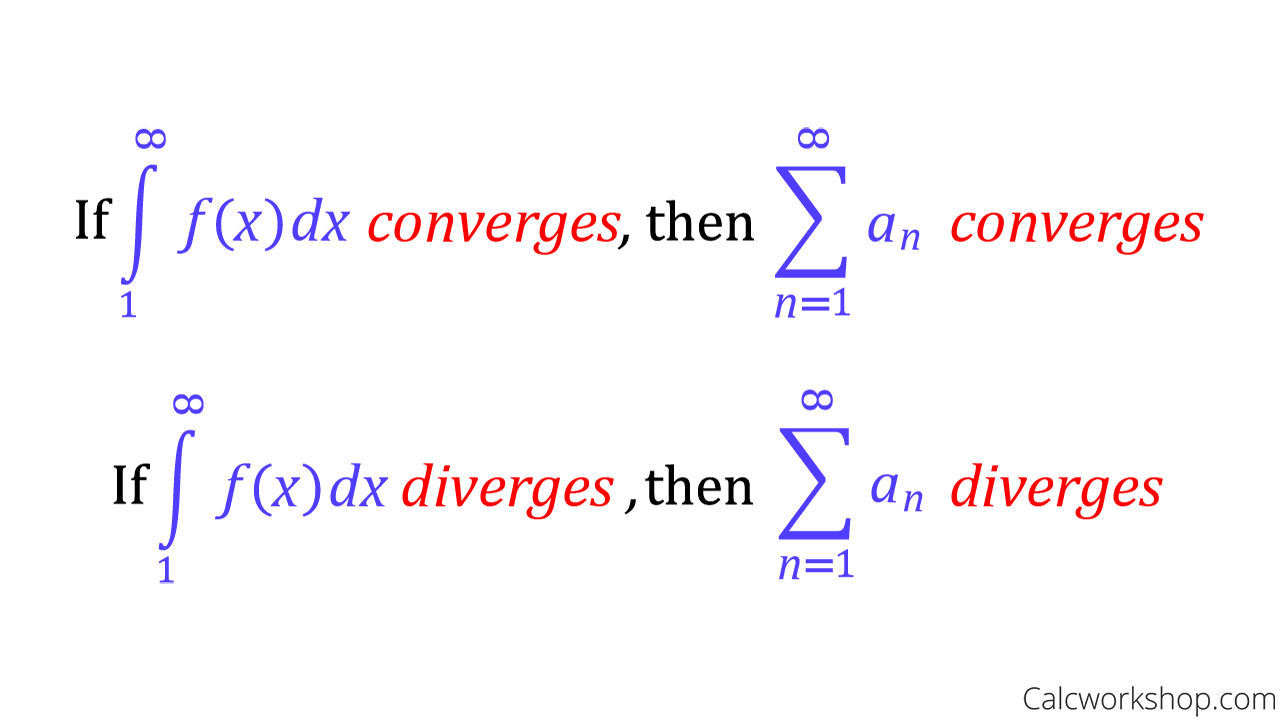

![[Resuelta] analisisreal ¿Por qué la convergencia es](http://i.stack.imgur.com/4Eecm.png)