Image Definition Math
Image Definition Math - In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\).
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\).
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\).
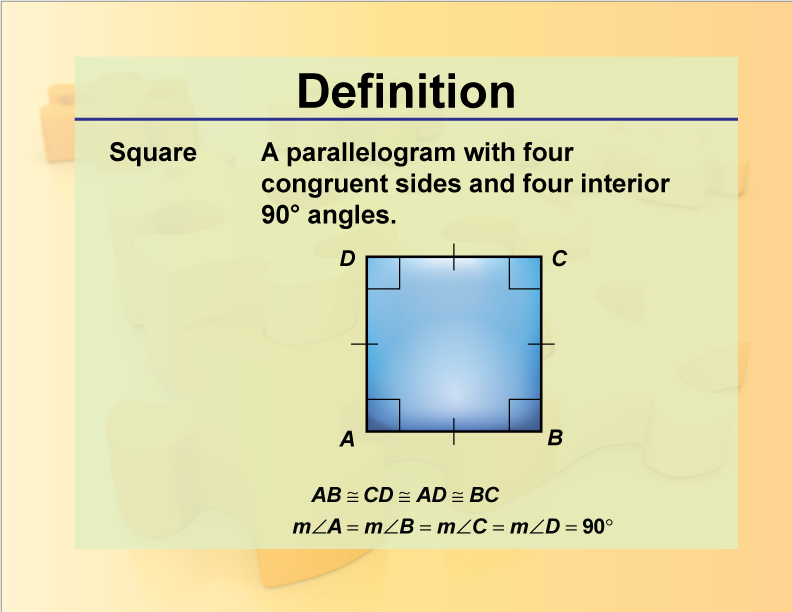
DefinitionGeometry BasicsSquare Media4Math
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is.
Identity Property in Math Definition and Examples
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
Whole Numbers Definition and Examples in Math in 2022 Number
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is.
"Nabla Operator Definition Math And Calculus Basics" Poster for Sale
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set.
Math Mean Definition
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is.
DefinitionMath PropertiesIdentity Element for Multiplication
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set.
ज्ञानगंगोत्री MATHS
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
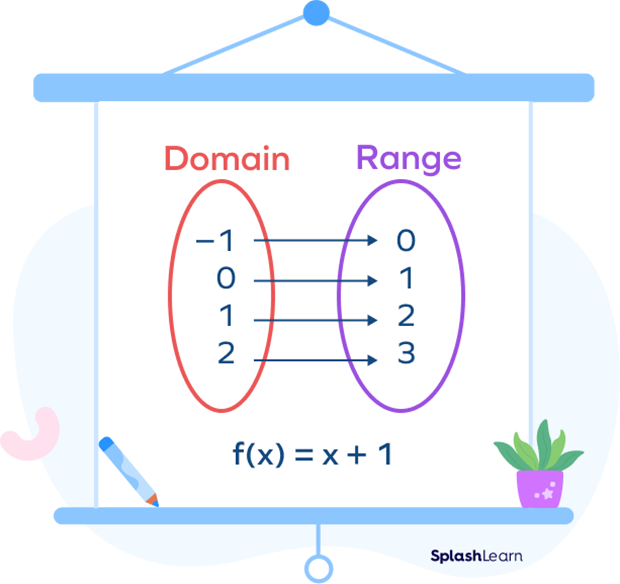
Range Math Definition
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
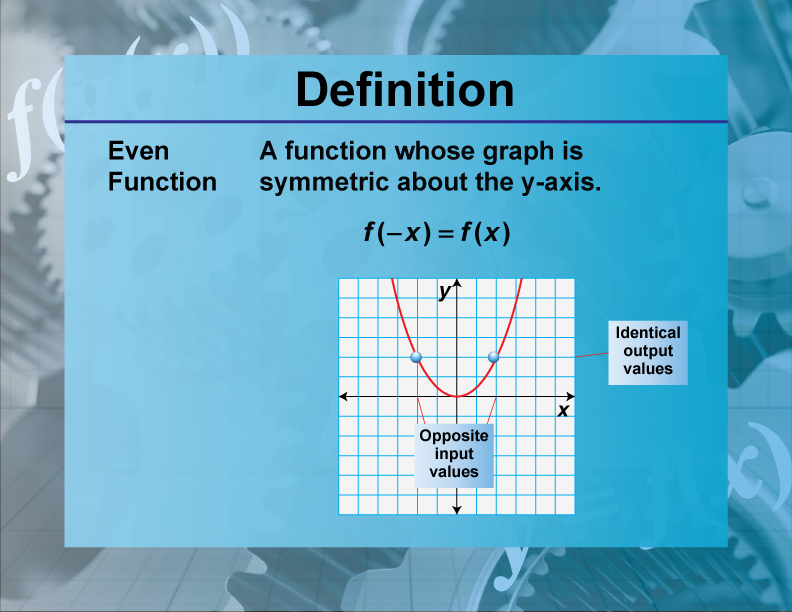
Function Math Definition
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
Solution Math Definition Example
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
The Image Of \(A_{1}\) Under \(F\) Is \[F\Left(A_{1}\Right)=\Left\{F(A) \Mid A \In A_{1}\Right\}.\] It Is A Subset Of \(B\).
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it.