What Makes A Vector Field Conservative
What Makes A Vector Field Conservative - Explain how to find a potential function for a conservative vector field. Use the fundamental theorem for line integrals to evaluate a line. The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. The gradient theorem for line integrals; In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. How to determine if a vector field is conservative;
How to determine if a vector field is conservative; The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. The gradient theorem for line integrals; We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. Explain how to find a potential function for a conservative vector field. In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. Use the fundamental theorem for line integrals to evaluate a line.
Explain how to find a potential function for a conservative vector field. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. Use the fundamental theorem for line integrals to evaluate a line. How to determine if a vector field is conservative; The gradient theorem for line integrals; The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =.
APMA E2000 Conservative Vector Fields & FTLI
We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. How to determine if a vector field is conservative; In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. Use the fundamental theorem for line integrals to evaluate.
Determinación de la función potencial de un campo vectorial conservador
The gradient theorem for line integrals; Use the fundamental theorem for line integrals to evaluate a line. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. How.
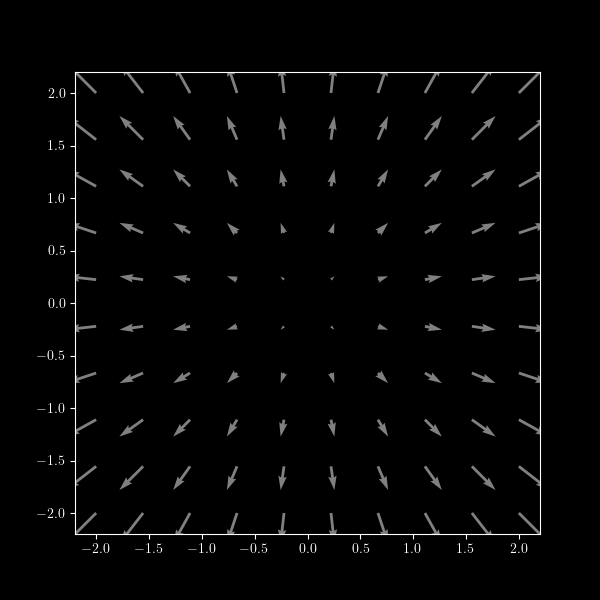
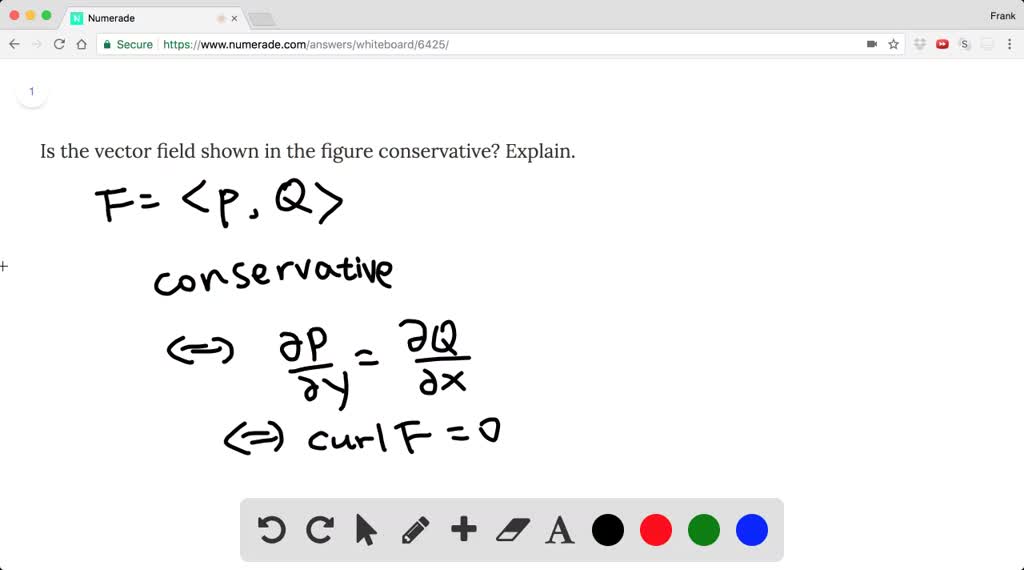
Is the vector field conservative? Explain. (GRAPH…
We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. The gradient theorem for line integrals; In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. Explain how to find a potential function for a conservative vector field..
The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. How to determine if a vector field is conservative; We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. Use the fundamental theorem for line integrals to evaluate.
Conservative Vector Fields YouTube
Explain how to find a potential function for a conservative vector field. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals. The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. How to determine if a vector.
potential function of a conservative vector field Vector Calculus
How to determine if a vector field is conservative; Explain how to find a potential function for a conservative vector field. In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus.
Bln The Natural Blog
The gradient theorem for line integrals; How to determine if a vector field is conservative; In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. Use the fundamental theorem for line integrals to evaluate a line. The vector field \(\vecs{f} \) is said to be conservative if there exists a.
Conservative vector field Alchetron, the free social encyclopedia
The gradient theorem for line integrals; In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. Explain how to find a potential function for a conservative vector field. How to determine if a vector field is conservative; We examine the fundamental theorem for line integrals, which is a useful generalization.
What is a Conservative Vector Field? Wait, What is a Vector Field
The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. The gradient theorem for line integrals; Explain how to find a potential function for a conservative vector field. Use the.
Curl and Showing a Vector Field is Conservative on R_3 YouTube
The vector field \(\vecs{f} \) is said to be conservative if there exists a function \(\varphi\) such that \(\vecs{f} =. In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to.
Use The Fundamental Theorem For Line Integrals To Evaluate A Line.
How to determine if a vector field is conservative; In this section we will take a more detailed look at conservative vector fields than we’ve done in previous sections. The gradient theorem for line integrals; Explain how to find a potential function for a conservative vector field.
The Vector Field \(\Vecs{F} \) Is Said To Be Conservative If There Exists A Function \(\Varphi\) Such That \(\Vecs{F} =.
We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals.